通俗来讲,最小生成树就是在一张图上,找到一棵生成树,这棵生成树的权值和最小。
而wiki中的解释为:最小生成树是一副连通加权无向图中一棵权值最小的生成树。这里需要注意几个点:
1.无向图。树一定是无向的
2.权值最小。权值最大时是最大生成树
3.连通图。不能搞成森林。
一般我们求最小生成树的时候有两个算法,prim和kruscal。
1.kruscal算法
这个算法比较好理解,考虑一张无向图G,里面有n个点m条边。我们只需要找到n-1条边组成生成树即可。因为是最小生成树,只要找到n-1条权值和最小的边就行了。按照贪心的思想,我们对边从小到大排序,再从中选出n-1条边生成一棵树就行了。选边的过程中,要用并查集维护联通块判环,使得生成的联通图是一棵树。
复杂度取决于排序算法,使用快速排序时复杂度为O(mlogm)。
2.prim算法
这个算法和dijkstra很像,甚至有些操作与dijkstra一样。具体的过程我放在下面的图里了。
朴素prim算法复杂度和dijkstra一样,为O(n^2)。如果使用邻接矩阵+优先队列,可以实现O(nlogm)的复杂度。
图在这里(感谢舍友的surface book 2)
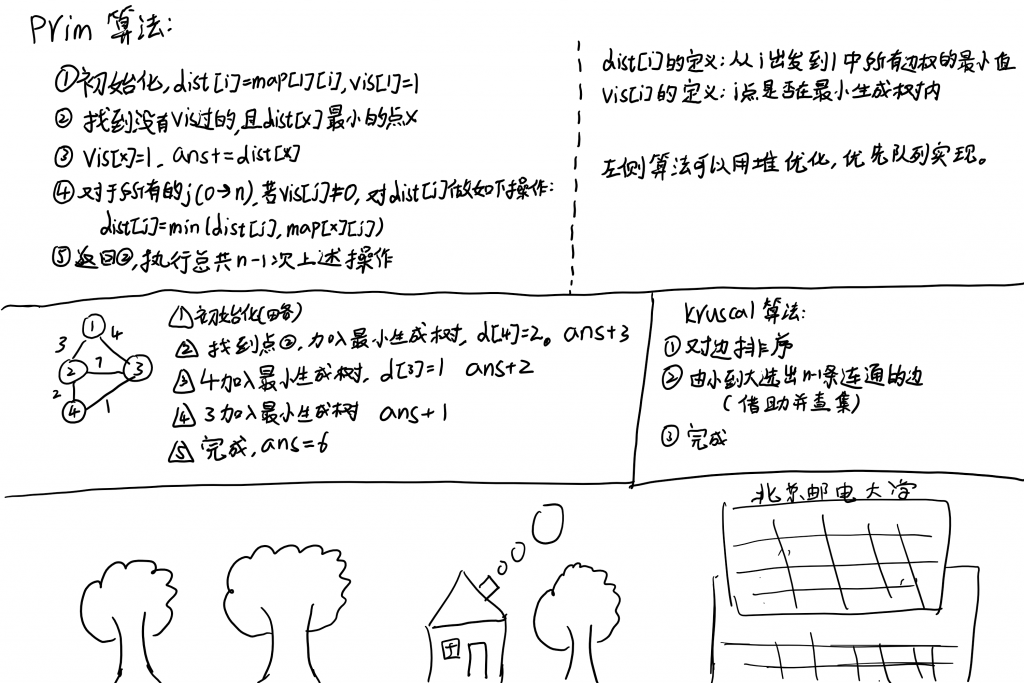
例题:
poj1251MST模板题
kruscal:
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; const int N=200; int fa[N]; int get(int x) { if(x==fa[x])return fa[x]; fa[x]=get(fa[x]); return fa[x]; } int tot=0; struct edge { int u,v,d; }s[N]; int n,m; bool cmp(edge a,edge b) {return a.d<b .d;} int main() { while(scanf("%d",&n)&&n>0) { tot=0; for(int i=1;i< =n;i++)fa[i]=i; for(int i=1;i<=n-1;i++) { char x[5];int cnt=0,y; scanf("%s%d",x,&cnt); int p=x[0]-'A'+1; for(int j=1;j<=cnt;j++) { scanf("%s%d",x,&y);int q=x[0]-'A'+1; s[++tot].u=p;s[tot].v=q;s[tot].d=y; s[++tot].v=p;s[tot].u=q;s[tot].d=y; } } int ans=0; sort(s+1,s+tot+1,cmp); for(int i=1;i<=tot;i++) { int a=s[i].u,b=s[i].v,d=s[i].d; if(get(a)==get(b))continue; ans+=s[i].d; fa[get(b)]=get(a); } printf("%d\n",ans); } return 0; }
堆优化(优先队列)prim:
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<queue> using namespace std; const int N=200; int head[N],nxt[N],list[N],len[N],tot; void add(int a,int b,int c) { tot++; list[tot]=b,len[tot]=c; nxt[tot]=head[a]; head[a]=tot; } struct pos { int a,d; pos(int xx,int dd){a=xx,d=dd;} friend bool operator< (pos a,pos b) { return a.d>b.d; } }; bool vis[N]; int dist[N]; int n,m; int prim() { priority_queue<pos>q; for(int i=head[1];i;i=nxt[i]) { q.push(pos(list[i],len[i])); dist[list[i]]=len[i]; } vis[1]=1;dist[1]=0; int ret=0; for(int i=1;i<n ;i++) { while(!q.empty()) { pos x=q.top();q.pop(); if(vis[x.a])continue; ret+=dist[x.a]; // cout<<dist[x.a]<<endl; vis[x.a]=1; for(int i=head[x.a];i;i=nxt[i]) { int u=list[i]; if(dist[u]>len[i]) { dist[u]=len[i]; if(!vis[u]) q.push(pos(u,dist[u])); } } break; } } return ret; } int main() { while(scanf("%d",&n)&&n>0) { tot=0;memset(vis,0,sizeof vis); memset(dist,0x3f,sizeof dist); memset(head,0,sizeof head); for(int i=1;i< =n-1;i++) { char x[5];int cnt=0,y; scanf("%s%d",x,&cnt); int p=x[0]-'A'+1; for(int j=1;j<=cnt;j++) { scanf("%s%d",x,&y);int q=x[0]-'A'+1; add(p,q,y),add(q,p,y); } } printf("%d\n",prim()); } return 0; }
poj2031
题目的意思是在一个三维的空间中给出n个球体,球的球心和半径已知,现在要将所有的球连通起来,
两个球的花费是圆心距减去半径和(接触为0),问最小花费
这题题意不太好理解,要注意相切/相交时的权值为0。
然后prim算法即可。
/* 题目的意思是在一个三维的空间中给出n个球体,球的球心和半径已知,现在要将所有的球连通起来, 两个球的花费是圆心距减去半径和(接触为0),问最小花费 */ #include<iostream> #include<cstring> #include<algorithm> #include<cmath> #include<cstdio> using namespace std; const int N=105; const double eps=1e-8; double x[N],y[N],z[N],r[N]; int n; double pos(int p,int q) { double t=pow(x[p]-x[q],2)+pow(y[p]-y[q],2)+pow(z[p]-z[q],2); t=sqrt(t)-(r[p]+r[q]); if(t<eps )t=0; return t; } double dist[N];bool vis[N]; double prim() { vis[1]=1,dist[1]=0;double ans=0; for(int i=1;i< =n;i++)dist[i]=pos(1,i); for(int i=1;i<n;i++) { double mn=1e9;int x; for(int j=1;j<=n;j++) if(dist[j]<mn&&!vis[j])mn=dist[j],x=j; ans+=dist[x];vis[x]=1; for(int j=1;j<=n;j++) if(!vis[j]) dist[j]=min(dist[j],pos(x,j)); } return ans; } int main() { while(scanf("%d",&n)&&n) { memset(vis,0,sizeof vis); for(int i=1;i<=n;i++) cin>>x[i]>>y[i]>>z[i]>>r[i]; printf("%.3f\n",prim()); } return 0; } </eps></cstdio></cmath></algorithm></cstring></iostream>
poj2421
给一个村子修路,已知所有节点的坐标,且已知村子里有一些道路已经修好。把两个节点连接起来花费的代价为两个节点之间的距离。要求修一些道路,使得所有节点联通,求最小花费。
修好的道路=>权值为0,然后跑最小生成树。注意一点,这种完全图一定要prim!
#include<iostream> #include<cstring> #include<algorithm> #include<cstdio> using namespace std; const int N=105; int map[N][N]; int dist[N],vis[N]; int n,m; int prim() { int ans=0; for(int i=1;i< =n;i++)dist[i]=map[1][i];vis[1]=1; for(int i=1;i<n;i++) { int mn=0x3f3f3f3f,x; for(int j=1;j<=n;j++) if(!vis[j]&&mn>dist[j])mn=dist[j],x=j; vis[x]=1,ans+=dist[x]; for(int j=1;j< =n;j++) if(!vis[j]) dist[j]=min(dist[j],map[x][j]); } return ans; } int main() { scanf("%d",&n); for(int i=1;i<=n;i++)for(int j=1;j<=n;j++) scanf("%d",&map[i][j]); scanf("%d",&m); for(int i=1;i<=m;i++) { int a,b; scanf("%d%d",&a,&b); map[a][b]=map[b][a]=0; } printf("%d\n",prim()); }
poj1789
定义i,j两个字符串之间的距离为d(i,j)。d(i,j)=∑(s[i][a]==s[j][a]?1:0)
现在已知有n个字符串,求联通这n个字符串的最小生成树。
模板题~~
#include<iostream> #include<cstring> #include<algorithm> #include<cstdio> using namespace std; const int N=2005,M=2*N*N; int tot,n; char t[N][10]; int map[N][N],dist[N],vis[N]; void build() { for(int i=1;i< =n;i++) for(int j=1;j<=n;j++) if(i!=j) { for(int k=1;k<=7;k++) map[i][j]+=(t[i][k]!=t[j][k]); } } int prim() { memset(dist,0,sizeof dist); for(int i=1;i<=n;i++)dist[i]=map[1][i]; memset(vis,0,sizeof vis); vis[1]=1;int ans=0; for(int i=1;i<n;i++) { int mn=0x3f3f3f3f,x=0; for(int j=1;j<=n;j++) if(dist[j]<mn&&!vis[j])mn=dist[j],x=j; ans+=mn,vis[x]=1; for(int j=1;j<=n;j++) if(!vis[j]) dist[j]=min(dist[j],map[x][j]); } return ans; } int main() { while(scanf("%d",&n)&&n) { memset(map,0,sizeof map); for(int i=1;i<=n;i++)scanf("%s",t[i]+1); build(); printf("The highest possible quality is 1/%d.\n",prim()); } return 0; }
poj1751
最小生成树,要求打印路径。
如果是kruscal,那么很容易,只需要把边集数组记录输出即可,但是这题要求prim(m很大)。
我们考虑每个点u被选入MST时,他所在的边<u,v>中的v点必定是最后一次对u进行松弛操作的点。所以我们只需要记录每个点被哪个点进行了最后一次松弛即可。据此,在加入最小生成树时推出其所在的边。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> using namespace std; const int N=1000; int x[N],y[N],vis[N],n,m; double dist[N]; int pre[N]; bool yes[N][N]; double d(int a,int b) { if(yes[a][b])return 0.0; return sqrt(pow(x[a]-x[b],2)+pow(y[a]-y[b],2)); } int ansx[N],ansy[N]; void prim() { double xmn=1e9;int k; memset(pre,0,sizeof pre); for(int i=1;i< =n;i++) { dist[i]=d(1,i);pre[i]=1; } memset(vis,0,sizeof vis);vis[1]=1; for(int i=1;i<n;i++) { int x; double mn=1e9; for(int j=1;j<=n;j++) if(!vis[j]&&mn>dist[j])mn=dist[j],x=j; vis[x]=1;ansx[i]=pre[x],ansy[i]=x; for(int j=1;j< =n;j++) if(!vis[j]) { if(dist[j]>d(x,j)) { dist[j]=d(x,j); pre[j]=x; } } } } int main() { scanf("%d",&n); for(int i=1;i< =n;i++) scanf("%d%d",&x[i],&y[i]); scanf("%d",&m); memset(yes,0,sizeof yes); for(int i=1;i<=m;i++) { int a,b;scanf("%d%d",&a,&b); yes[a][b]=yes[b][a]=1; } prim(); for(int i=1;i<n;i++) if(!yes[ansx[i]][ansy[i]]) printf("%d %d\n",ansx[i],ansy[i]); return 0; }
poj3026
已知一张地图,上面有很多宝藏。一队探险队从s点出发,不能穿过墙,并要求到达所有的宝藏。可以在任意一点把探险队分为两队或多队。求探险队走过的总距离的最小值。
其实就是这张图上宝藏和s点的最小生成树!
先以每个点为起点对全图进行bfs,得到该点到每个宝藏点和s点的最短距离,并且对宝藏点和s点编号,然后跑prim算法。
#include<iostream> #include<algorithm> #include<cstring> #include<cstdio> #include<queue> using namespace std; const int N=70; char map[N][N]; int dx[4]={1,0,-1,0}; int dy[4]={0,1,0,-1}; int dist[N*N]; int a[N*N][N*N],va[N*N],d[N][N]; struct pos { int x,y,d; pos(){}; pos(int a,int b,int c) {x=a,y=b,d=c;} }; int vis[N][N],cvis; inline int gp(int a,int b) { if(vis[a][b]==0)vis[a][b]=++cvis; return vis[a][b]; } int n,m; bool judge(int x,int y) { if(x<1||y<1||x>n||y>m)return 0; return 1; } void bfs(int sa,int sb) { queue<pos>q;q.push(pos(sa,sb,0)); memset(d,0,sizeof d); d[sa][sb]=-1; while(!q.empty()) { pos v=q.front();q.pop(); int a=v.x,b=v.y; for(int i=0;i<4;i++) { int a=v.x+dx[i],b=v.y+dy[i]; if(d[a][b]==0&&judge(a,b)&&map[a][b]!='#') { d[a][b]=v.d+1; q.push(pos(a,b,v.d+1)); } } } d[sa][sb]=0; int v=gp(sa,sb); for(int i=1;i< =n;i++) for(int j=1;j<=m;j++) if(map[i][j]=='A'||map[i][j]=='S') { int u=gp(i,j); a[v][u]=d[i][j]; } } int prim(int s) { memset(dist,0x3f,sizeof dist); memset(va,0,sizeof va); va[s]=1;int ret=0; for(int i=1;i<=cvis;i++)dist[i]=a[s][i]; for(int i=1;i<=cvis-1;i++) { int mn=0x3f3f3f3f,x=0; for(int i=1;i<=cvis;i++) if(!va[i]&&mn>dist[i])mn=dist[i],x=i; ret+=mn;va[x]=1; for(int i=1;i< =cvis;i++) if(!va[i]&&dist[i]>a[x][i])dist[i]=a[x][i]; } return ret; } char tttt[100]; int main() { int t;scanf("%d",&t); while(t--) { cvis=0; memset(vis,0,sizeof vis); scanf("%d%d",&m,&n); gets(tttt); for(int i=1;i< =n;i++)gets(map[i]+1); int q=0; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(map[i][j]=='S'||map[i][j]=='A') { bfs(i,j); if(map[i][j]=='S')q=gp(i,j); } /* cout<<cvis<<endl; for(int i=1;i<=cvis;i++) for(int j=1;j<=cvis;j++)cout<<a[i][j]<<endl;*/ printf("%d\n",prim(q)); } return 0; }
poj1679
问最小生成树是否唯一。
第一种方法:求次小生成树。
我们假设最小生成树不唯一,那么我们删掉最小生成树上的某条边之后,可以用其它不在最小生成树上的边替代它,所以,我们枚举最小生成树P上的每一条边i,删除边i后再求最小生成树,得到生成树Q,倘若P的权值等于Q的权值,那么最小生成树就不唯一。若不存在这样的Q,那么最小生成树唯一。
代码:
#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> using namespace std; const int N=705,M=N*N; struct edge { int a,b,c; }s[M]; bool cmp(edge a,edge b) { return a.c<b .c; } int fa[N]; int t,n,m; bool vis[M]; int find(int p){if(fa[p]!=p)fa[p]=find(fa[p]);return fa[p];} void uni(int a,int b) { if((a=find(a))==(b=find(b)))return; fa[a]=b; } bool judge() { int cnt=0; for(int i=1;i<=n;i++) if(fa[i]==i)cnt++; return cnt>1; } int kru(int del) { int ans=0,cnt=1; for(int i=1;i< =m;i++) { if(cnt==n)break; if(i==del)continue; int a=find(s[i].a),b=find(s[i].b); if(a==b)continue; uni(a,b); if(del==0) vis[i]=1; ans+=s[i].c; cnt++; } //cout<<"ans: "<<ans<<endl; return ans; } void work() { sort(s+1,s+m+1,cmp); int e=kru(0); if(judge())puts("0"); bool flag=1; for(int i=1;i<=m;i++) { if(!vis[i])continue; for(int j=1;j<=n;j++)fa[j]=j; int k=kru(i); if(judge())continue; if(k==e){flag=0;break;} } if(flag)printf("%d\n",e); else puts("Not Unique!"); } void init() { memset(vis,0,sizeof vis); memset(&s,0,sizeof s); for(int i=1;i<=n;i++)fa[i]=i; } int ca; int main() { scanf("%d",&ca); while(ca--) { scanf("%d%d",&n,&m); init(); for(int i=1;i<=m;i++) scanf("%d%d%d",&s[i].a,&s[i].b,&s[i].c); work(); } return 0; }
第二种方法:倍增LCA或树链剖分。
我们假设存在次小生成树,那么次小生成树一定是最小生成树上一条权值较大的边被替换的得到的(权值越小越不容易被替换),那么我们有一下算法。
我们还是按刚刚的方法,先求最小生成树。再在最小生成树上做倍增。对于每条不在最小生成树上的边<u,v>,我们在最小生成树上查询u,v之间的最大边。若最大边的权值等于边<u,v>的权值,那么就可以用<u,v>替换这条边,也就是存在第二个最小生成树。
代码:
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> using namespace std; const int N=105,M=N*N; int head[N],nxt[M],list[M],len[M],tot; int n,m,t; void add(int a,int b,int c) { tot++; list[tot]=b,len[tot]=c; nxt[tot]=head[a]; head[a]=tot; } int d[N],fa[N][10],g[N][10],vis[N]; void dfs(int a) { vis[a]=1; for(int i=head[a];i;i=nxt[i]) { int x=list[i]; if(!vis[x]) { d[x]=d[a]+1; g[x][0]=len[i]; fa[x][0]=a; dfs(x); } } } void zeng() { for(int i=1;i< =n;i++) for(int j=1;j<=8;j++) { fa[i][j]=fa[fa[i][j-1]][j-1]; g[i][j]=max(g[i][j-1],g[fa[i][j-1]][j-1]); } } int query(int a,int b)//find min edge of (a,b) { int ret=-0x3f3f3f3f; if(d[a]>d[b])swap(a,b); if(d[a]<d [b]) { int del=d[b]-d[a]; for(int i=0;i<=8;i++)//binary split if(del&(1<<i)) { ret=max(ret,g[b][i]); b=fa[b][i]; } } if(a==b)return ret; for(int i=8;i>=0;i--) { if(fa[a][i]!=fa[b][i]) { ret=max(ret,max(g[b][i],g[a][i])); a=fa[a][i],b=fa[b][i]; } } ret=max(ret,max(g[a][0],g[b][0])); return ret; } int f[N]; int get(int x) { if(x==f[x])return f[x]; f[x]=get(f[x]); return f[x]; } struct edge { int x,y,d; }s[M]; bool cmp(edge a,edge b) {return a.d<b .d;} int have[N],ans; void kru() { sort(s+1,s+m+1,cmp); for(int i=1;i<=m;i++) { int a=get(s[i].x),b=get(s[i].y); if(a==b)continue; add(s[i].x,s[i].y,s[i].d); add(s[i].y,s[i].x,s[i].d); f[b]=a;have[i]=1; ans+=s[i].d; } // cout<<ans<<endl; } bool work() { dfs(1); zeng(); for(int i=1;i<=m;i++) { if(!have[i]) { if(query(s[i].x,s[i].y)==s[i].d) { // cout<<s[i].x<<" "<<s[i].y<<" "<<query(s[i].x,s[i].y)<<" "<<s[i].d<<endl; return 0; } } } return 1; } int main() { // freopen("out.txt","w",stdout); int cnt=0; scanf("%d",&cnt); while(cnt--) { ans=tot=n=t=m=0; memset(head,0,sizeof head); memset(vis,0,sizeof vis); memset(have,0,sizeof have); memset(fa,0,sizeof fa); memset(g,0,sizeof g); memset(d,0,sizeof d); scanf("%d%d",&n,&t); for(int i=1;i<=n;i++)f[i]=i; for(int i=1;i<=t;i++) { int a,b,c; scanf("%d%d%d",&a,&b,&c); s[++m].x=a,s[m].y=b,s[m].d=c; // s[++m].x=b,s[m].y=a,s[m].d=c; } kru(); if(work())printf("%d\n",ans); else puts("Not Unique!"); } return 0; }
第三种方法:玄学贪心
两遍克鲁斯卡尔。第一遍正常做,然后给所有在最小生成树上的边打上标记。第二遍,排序时,未打标记的边优先选用。若两次最小生成树权值相等,且边不等,则存在相同的最小生成树。
代码:难受,不写!!
差不多就是这样了,可能还会再补充一点高级的知识。